编译原理
tt版本
正则表达式

基础的正则表达式。L(r)表示正则表达式r所表述的语言

基本的符号包括了 | * 连接
正则定义式如下形式的定义序列
d1 → r1
d2 → r2
dn → rn
扩展运算符

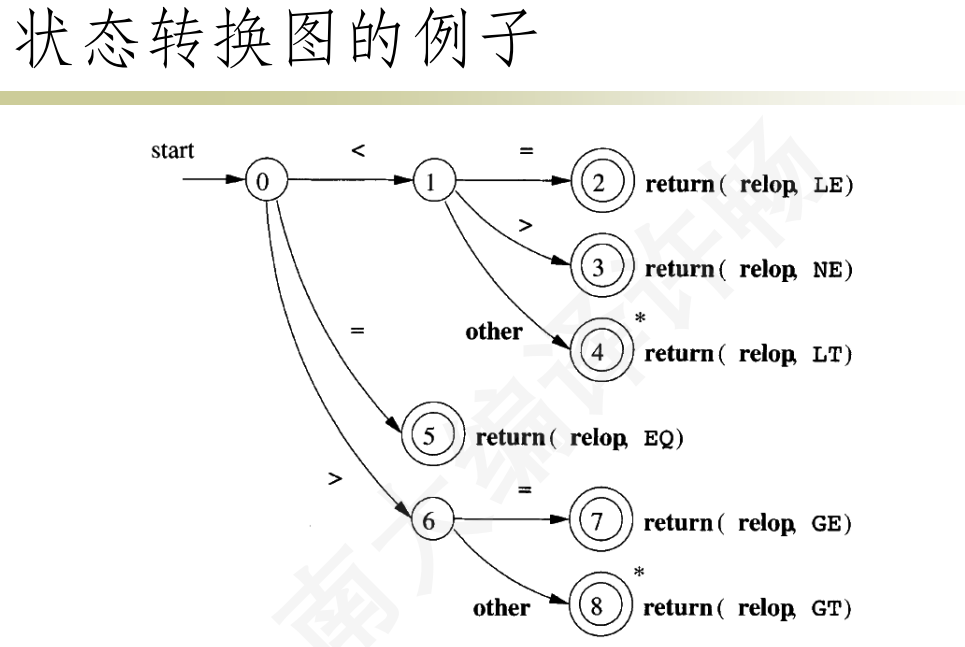
状态转换图
点->state 边->转换
词法分析工具:Lex/Flex
Contents
词法分析部分重要知识点
DFA和NFA的区别
NFA:非确定有限自动机
DFA:确定有限自动机
NFA在同一状态,可以有多条出边,DFA在同一状态,只能有一条出边;
NFA的初态可以具有多个,DFA的初态是唯一的;
语言是给定字母表Σ上一个任意的可数的串集合。
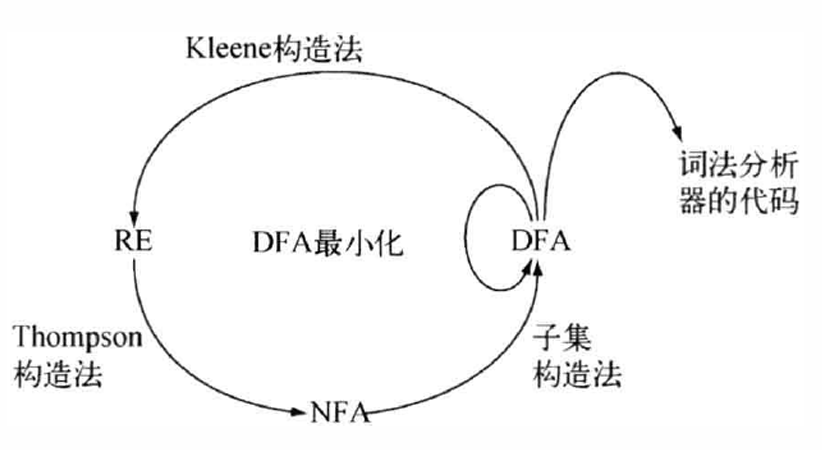
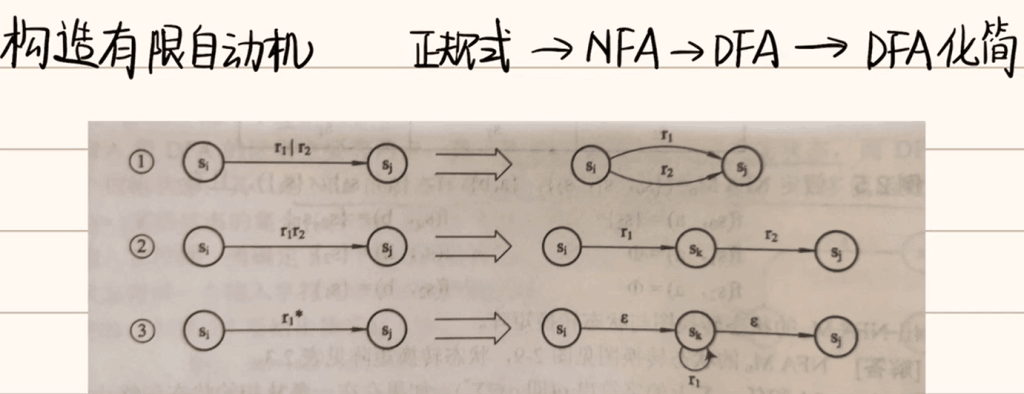
Thompson构造法
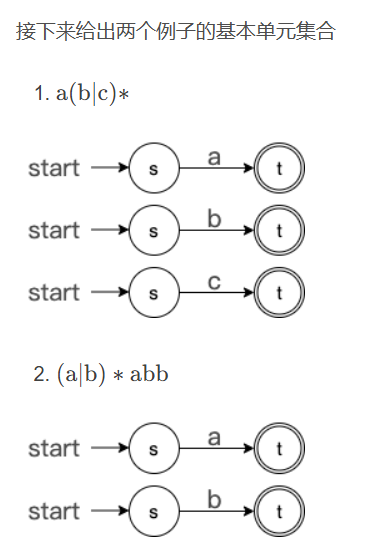
接下来就进入本篇的重点:Thompson 构造法(正则表达式 -> NFA)
Thompson 构造法将定义基本单元以及三种合并基本单元的原则,接下来我们使用两个正则表达式作为例子逐步构造
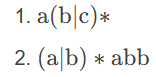
Thompson 构造法的第一步就是先构建所有基本单元,这边我们就为符号表中的每一个 符号 c ∈ ∑ 构建一个基本单元
重要的转换规则
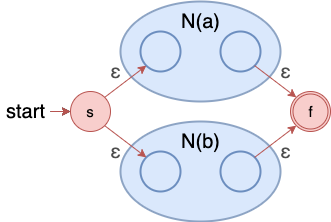
并:a ∣ b
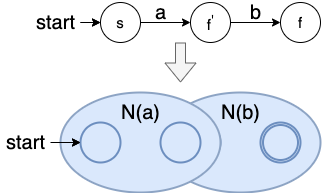
连接:a b
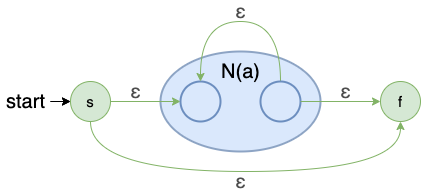
闭包:a ∗
DFA构造

Subset-Construction(NFA)
let Dtran be a table
DFA_States = {ε-closure(NFA.s0)} # DFA 状态集合的初始状态为 NFA 初始状态的闭包,并且未标记
while (exist T in DFA_States not marked) { # 存在未标记的 DFA 状态
mark T # 标记 T,表示查过 T 状态的所有后续状态了
for (a in Σ) {
Tc = ε-closure(move(T, a)) # 找到所有输入字符对应的下一个状态
if (Tc not in DFA_States) { # 将状态加入到 DFA_States
push Tc in DFA_States & unmarked Tc
}
Dtran[T, a] = Tc
}
}
return Dtran以上为构造DFA子集的伪代码实现
接下来我们按照编译原理: Subset Construction 子集构造法(幂集构造)(NFA转DFA)_编译原理nfa转dfa-CSDN博客逐步讲解DFA的子集构造法构造流程
首先我们先求出起始 DFA 状态设为 A
第二步找到未标记状态A,可以输入的字符为a
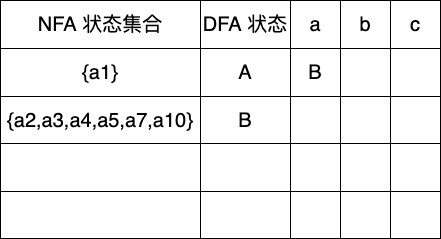
下一个未标记状态为B,可输入字符有b,c
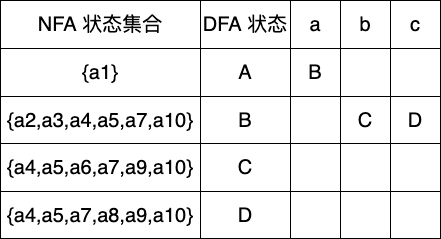
下一个状态C,可能输入的字符有b,c
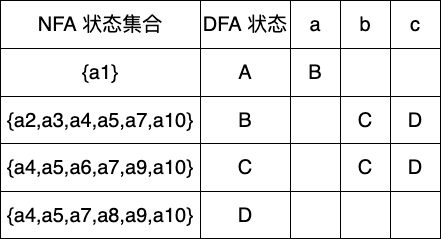
下一个状态D,可输入字符还是b,c
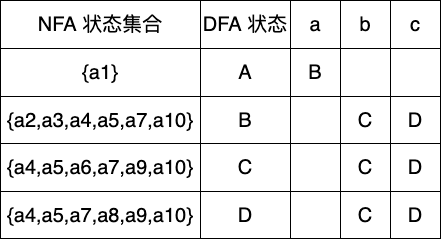
其实到此我们已经完成 DFA 的构建了,Dtran 表就是一种也是应用时使用的 DFA 转换函数表,现在我们根据构建好的 Dtran 表绘制出对应的 DFA
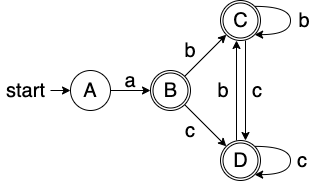
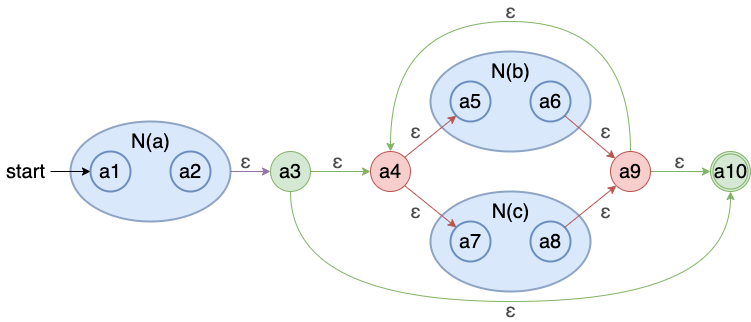
构造NFA的例题

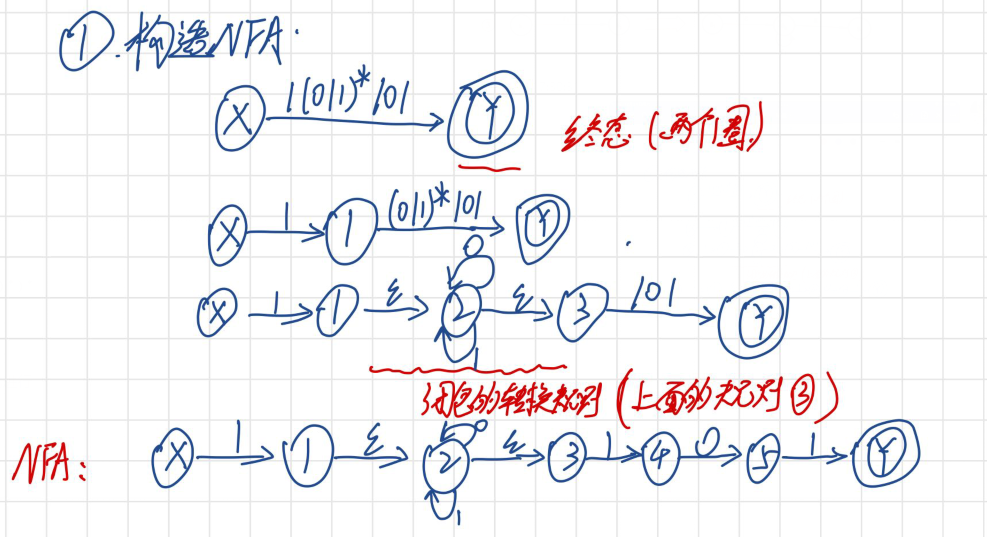
把NFA通过子集构造法转换为DFA
方法介绍:首先我们通过Thompson构造法把正则表达式转换为“不确定有限状态机”NFA,接下来我们需要通过子集构造法的方式把NFA再转换为DFA(NFA转DFA的子集构造(subset construction)算法 – 简书 (jianshu.com))

获得了正常的DFA图之后,我们就需要考虑:这样的状态转移图如何可以最小化(即合并等价状态)
首先:如何定义等价状态?
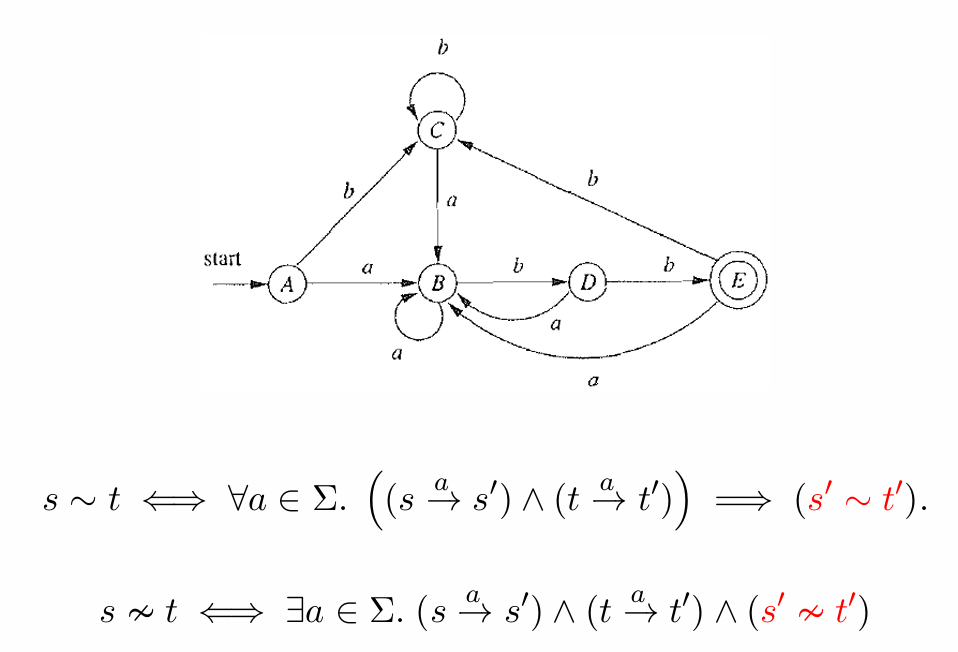
但是按照这个推论,我们无法得到“最初始的”等价的两个状态,所以无法进展。我们因此反过来想,根据第二个定理,我们可以划分不等价的区间(因为接收状态与非接受状态必然不等价,所以这是可以开始的)

再另外举个例子:(7是非接受态)
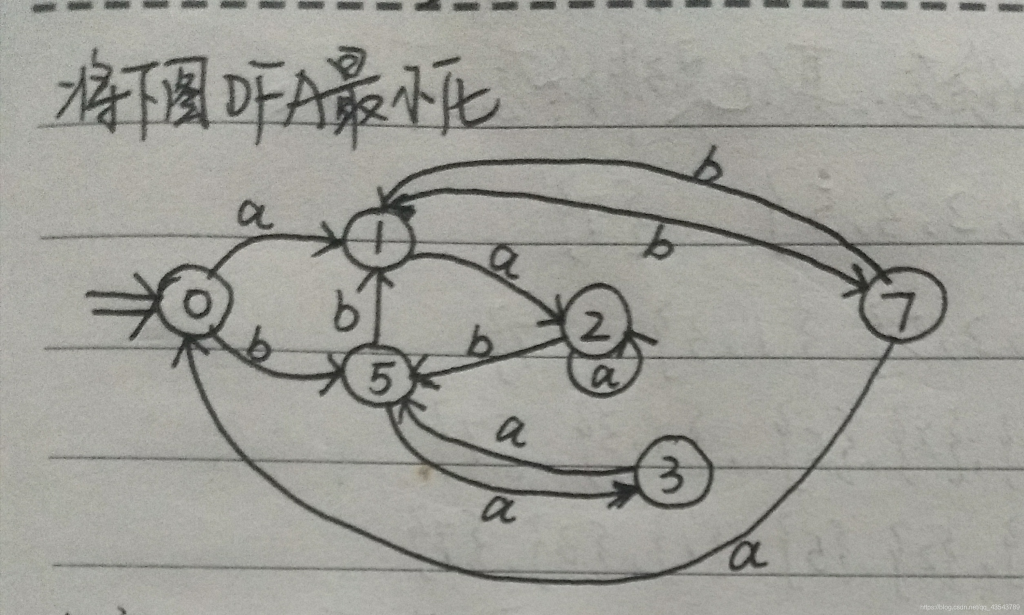

最小化确定有限状态自动机(DFA)的过程涉及以下几个步骤:
- 识别和标记不可区分的状态对:
首先,我们通过识别不可区分的状态对开始最小化过程。不可区分的状态对是那些无法通过任何输入区分的状态。 - 合并不可区分的状态:
根据不可区分的状态对,我们将它们合并以形成新的状态。这样做会减少DFA中的状态数。
让我们逐步讲解如何通过划分来最小化给定的DFA:
初始划分 (Π0)
我们首先根据是否为接受状态将状态分成两个组:
- 非接受状态:{A, B, C, D}
- 接受状态:{E}
所以初始划分为:
[ Π0 = {{A, B, C, D}, {E}} ]
第一步划分 (Π1)
我们检查每个状态在每个输入符号下的转换,并根据这些转换进一步划分状态。
对于状态A, B, C, D:
- 在输入a下,A和D转到B,B转到B,C转到B,这些状态仍然在同一组。
- 在输入b下,A和C转到C,B转到D,D转到E。这些转换结果位于不同组,因此需要进一步划分。
结果为:
[ Π1 = {{A, B, C}, {D}, {E}} ]
第二步划分 (Π2)
我们再次检查每个状态在每个输入符号下的转换。
对于状态A, B, C:
- 在输入a下,A转到B,B转到B,C转到B,这些状态仍然在同一组。
- 在输入b下,A转到C,B转到D,C转到C。这些转换结果位于不同组,因此需要进一步划分。
结果为:
[ Π2 = {{A, C}, {B}, {D}, {E}} ]
最终划分 (Π3)
我们再次检查每个状态在每个输入符号下的转换,确认是否还需要进一步划分。
对于状态A, C:
- 在输入a下,A转到B,C转到B,这些状态仍然在同一组。
- 在输入b下,A转到C,C转到C。这些转换结果位于同一组。
因此,划分不再变化,最终划分为:
[ Π3 = {{A, C}, {B}, {D}, {E}} ]
重新构建最小化DFA
根据最终划分,我们可以重建最小化的DFA。新的状态集为{AC, B, D, E},其中:
- 状态{A, C}合并为新状态AC
- B, D, E保持不变
新DFA的转换如下:
- 从AC出发,a转到B,b转到AC
- 从B出发,a转到B,b转到D
- 从D出发,a转到E,b转到E
- 从E出发,a和b都保持在E
新DFA可以如下图表示:
AC --a--> B
| |
b b
| |
v v
AC <--a-- D --a--> E
| |
b b
| |
v v
E E通过这个步骤,我们实现了DFA的最小化。
上下文无关文法(Context Free Grammar)
文法的形式定义:
规则:规则也称产生式,它是一个符号与一个符号串的有序对(A,),通常写做A→
( 或 A::=
)
其中 A 是规则左部,是一个符号;β是规则右部,是一个符号串。→ 或 ::= 表示“定义为”或“生成”,意思是左部符号用右部符号串定义或左部符号生成右部符号串。规则的作用是告诉如何用规则中的符号串生成语言中的序列。一组规则规定了一个语言的语法结构。
- 上下文无关文法G是一个四元组G=(T,N,P,S)):
- T是终结符号 Terminal集合, 对应于词法分析器产生的词法单元
- N是非终结符号 Non-terminal集合
- P是产生式 Production集合
- S是开始符号
文法是一组替换规则,例如下面的例子

在下面的例子中,有几个重要的概念:
- 变量 / 非终结符 (variable)
- 终结符(teminals)
- 句子(sentence)
- 句型(sentential forms):变量 + 终结符
- 我们把使用上下文无关文法表示的语言称为上下文无关语言;有些 context-free 语言并不是 regular 的例如 { 0^n*1^n ∣ n ≥ 1 }
TIP:
包含给定的元素 , 并且 具有指定性质 的 最小的 集合 , 称为关系的闭包 ; 这个指定的性质就是关系 R
自反闭包 r ( R ) : 包含 R 关系 , 向 R 关系中 , 添加有序对 , 变成 自反 的 最小的二元关系
对称闭包 s ( R ) : 包含 R 关系 , 向 R 关系中 , 添加有序对 , 变成 对称 的 最小的二元关系
传递闭包 t ( R ) : 包含 R 关系 , 向 R 关系中 , 添加有序对 , 变成传递 的 最小的二元关系
上下文无关文法举例
- 一个符号要么是终结符号,要么是非终结符号
- 终结符号表示到此为止,无法再进行替换

条件语句文法
- 条件语句文法中包含悬空(Dangling)-else文法的问
- 这样的文法是有问题,我们进一步分析才可以,OTHER作为终结符。
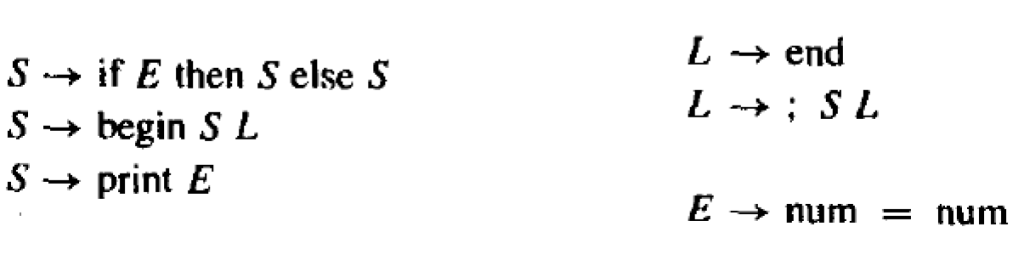
关于终结符号的约定
- 在字母表里排在前面的小写字母,比如a、b、c。
- 运算符号,比如+、*等。
- 标点符号,比如括号、逗号等。
- 数字,0、1、… 9。
- 黑体字符串,比如id或if。每个这样的字符串表示一个终结符号。
关于非终结符号的约定
下述符号是非终结符号:
- 在字母表中排在前面的大写字母,比如A、B、C。
- 字母S。它出现时通常表示开始符号。
- 小写、斜体的名字,比如expr或stmt
例题:

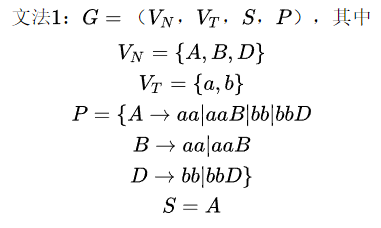

例3
用文法定义一个含+、*、()的算术表达式。
分析:变量是表达式;若 E1 和 E2 是算术表达式,则 E1+E2,E1*E2,(E) 也是算术表达式。
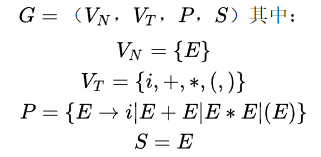
推导(Deviation)
令 G 是一文法,一步推导 => 表示用某一规则的右部替换其左部。如果有 xAy => xαy,仅当 A→α 是 G 的一个规则(产生式),且 x、y ∈
称 xAy 直接推出 xαy。


直接推导的长度为1,推导的长度大于等于1,广义推导的长度大于等于0
句型(Definition)与句子(Sentence)

关于文法G的两个基本问题
- Membership问题:给定字符串x∈T∗,x∈L(G)?字符串可不可以由文法推理得到
- L(G)究竟是什么?
文法的分类




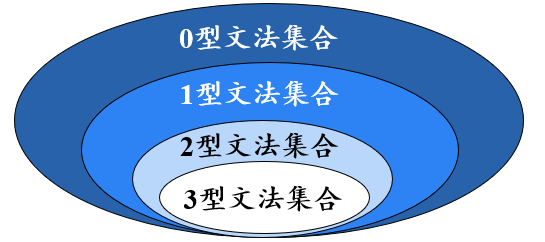
CFG的分析树
- 根节点的标号为文法开始符号
- 内部结点表示对一个产生式 A→β 的应用,该结点的标号是此产生式左部 A 。该结点的子结点的标号从左到右构成了产生式的右部β
- 叶结点的标号既可以是非终结符,也可以是终结符。从左到右排列叶节点得到的符号串称为是这棵树的产出 (yield) 或边缘 (frontier)
给定一个句型,其分析树中的每一棵子树的边缘称为该句型的一个短语 (phrase)
如果子树只有父子两代结点,那么这棵子树的边缘称为该句型的一个直接短语 (immediate phrase)
问题一:Membership问题
这就是语法分析器的任务:为输入的词法单元流寻找推导、构建语法分析树, 或者报错
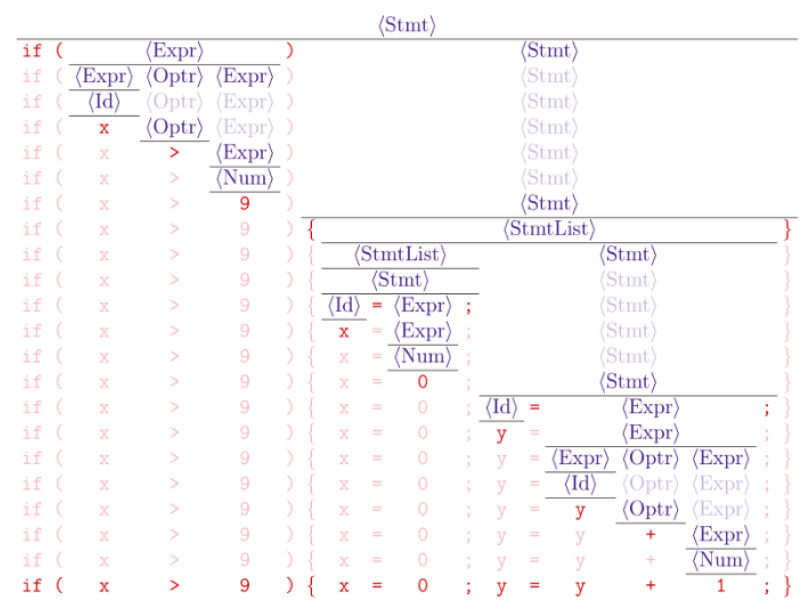
问题二:L(G) 是什么?
根据文法G推导语言L(G)

根据语言L(G)来推导文法G

LL(1)、LL(k)&all-star
自顶向下的、递归下降的、预测分析的、适用于LL(1)文法的LL(1)语法分析器
其中的“1”指的是只看一个标记,简化分析过程,常使用递归下降方法实现

S→F
S→(S+F)
F→a
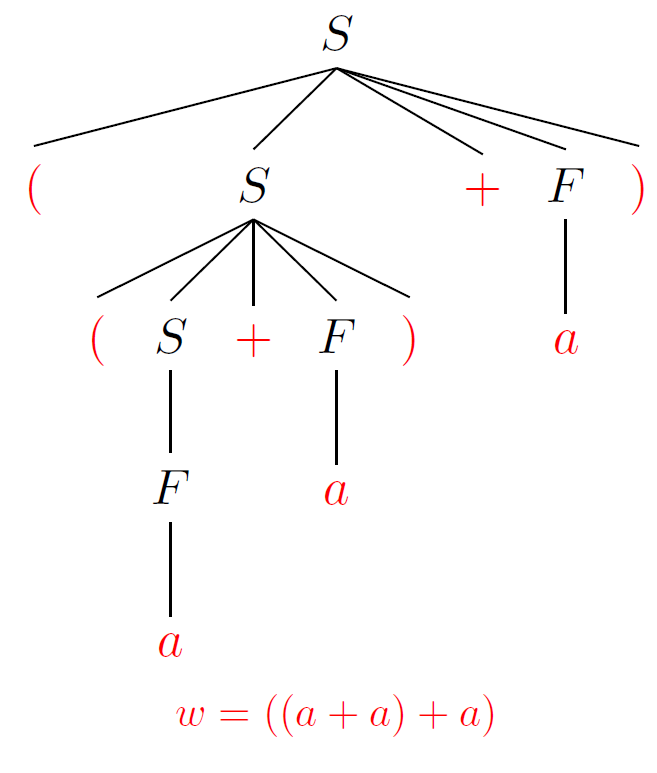
- 每次都选择语法分析树最左边的非终结符进行展开,所以得到最左推导
- Q:同样是展开非终结符S,为什么前两次选择了S→(S+F)𝑆→(𝑆+𝐹)S→(S+F), 而第三次选择了S→FS→F?
- A:因为只有选择S→(S+F) S→(S+F)才能生成一个左括号开头的式子,这个是由文法决定的,也就是因为它们面对的当前词法单元不同
使用预测分析表确定产生式
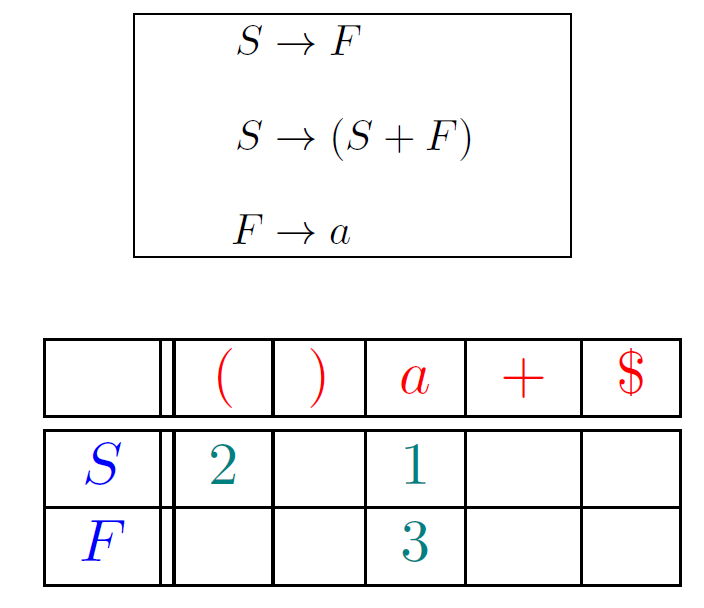
指明了每个非终结符在面对不同的词法单元或文件结束符时,该选择哪个产生式(按编号进行索引)或者报错
如何构建预测分析表:
- 确定候选产生式:对于表中的每一对非终结符和终结符,找出所有可能的候选产生式。
- 选择最具体的产生式:如果只有一个候选产生式,则直接将其放入单元格中。
- 解决冲突:如果有多个候选产生式,需要根据特定的规则来解决冲突。在LL(1)分析中,每个单元格中只能有一个产生式。
举例说明:
假设我们有以下文法:
E -> E + T {产生式1}
E -> T {产生式2}
T -> T * F {产生式3}
T -> F {产生式4}
F -> ( E )
F -> id {产生式5}这里的非终结符是 E, T, F,终结符是 +, *, (, ), id 和 EOF。
预测分析表可能如下所示:
+ * ( ) id
E {1} {2} - - - -
T - {3} - - - -
F - - {4} {5} - -解释:
- 当栈顶是非终结符
E,下一个输入是+时,我们使用产生式1。 - 当栈顶是非终结符
E,下一个输入是*或id时,我们使用产生式2。 - 当栈顶是非终结符
T,下一个输入是*时,我们使用产生式3。 - 当栈顶是非终结符
T,下一个输入是(或id时,我们使用产生式4。 - 当栈顶是非终结符
F,下一个输入是(时,我们使用产生式5。
注意,表中的 - 表示没有适用的产生式,这通常意味着语法错误。
冲突解决:
如果表中的单元格有多个产生式,我们需要解决冲突。这可能涉及到文法的转换或分析策略的改变。在LL(1)文法中,每个单元格中只能有一个产生式,这是构建预测分析表的基本要求。
预测分析表是LL(1)分析器的核心,它使得编译器能够高效地进行语法分析,而无需进行复杂的回溯操作。
实现LL(1)算法的具体代码
解析S:
1: procedure S()
2: if token = '(' then
3: MATCH('(')
4: S()
5: MATCH('+')
6: F()
7: MATCH(')')
8: else if token ='a' then
9: F()
10: else
11: ERROR(token, {'(', 'a'})解析F
1: procedure F()
2: if token = 'a' then
3: MATCH('a')
4: else
5: ERROR(token, {'a'})解析MATCH()
1: procedure MATCH(t)
2: if token = t then
3: token <- NEXT-TOKEN
4: else
5: ERROR(token, t)Key:如何计算给定文法G的预测分析表
Definition(First(α)集合)
首先我们需要求出First集合,对于所有产生式的右部而言
对于任意的(产生式的右部) α∈(N∪T)∗
1、X∈VT (终结符号集合)
FIRST(X)={X}(即:终结符号的FIRST集仍然是其本身)。
2、X∈VN(非终结符号集合)
(1)若X→a…, 则 a 加入FIRST(X);若有X→ε,则ε加入 FIRST(X)(a是X可以推出的首个终结符号)。
(2)若有X→Y…, 且Y∈VN ,则FIRST(Y)中非ε元素全部加入FIRST(X);
(3)若有X→Y1Y2Y3…YK ,且Yi∈VN ,ε∈FIRST(Yj) ,则FIRST(Yi)中非ε元素加入FIRST(X);若所有的FIRST(Yj)都含有ε,则ε加入FIRST(X)。
另一种方式是:


例子:
使用一下文法测试算法
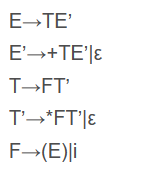
所以第一轮可以推出E‘和T’中各自有+,*和ε的终结符,F有(和i

第二轮中,E去找T的终结符(第一个推导式子),获得nothing,E‘也不行,T能找到F的(和i,

第三轮,E找T找到了,更新成一样的(和i,E‘等等都找不到,也没有连续含空的情况,所以本轮结束之后的每一轮都没变化,结束


为每个非终结符X计算Follow(X)集合
定义的大白话:对于某个非终结符,紧跟在其后面的终结符的集合就是这个非终结符的Follow集

构造Follow集合有以下几种情况:
E->...Ab...,即在产生式中任意位置存在 一个非终结符 + 一个终结符,则将终结符加入到非终结符的Follow集合中,即Follow(A)<==bE->...AB...,即在产生式中存在 两个非终结符相邻,且B不在末尾,则将B的First集合减去ε再加入到A的Follow集合中,即Follow(A)<==First(B)-εE->...AB,即在产生式中存在 两个非终结符相邻,且B在末尾,此时分为两种情况:B!=>*ε,即B不能推出ε时,需将B的First-ε集加入A的Follow集,且将E的Follow集加入B的Follow集合。即Follow(A) <== First(B) – ε,Follow(B) <== Follow(E)B=>*ε,即经过若干步的推导B能推导出ε,则不仅需要将B的Follow集加入A的Follow集,E的Follow集加入B的Follow集合,还需要将E的Follow集合加入A的Follow集合。即Follow(A) <== First(B) – ε+Follow(E),Follow(B) <== Follow(E)。
E->TA
A->+TA|ε
T->FB
B->*FB|ε
F->i|(E)Follow(E)={),#}
Follow(A)={),#}
Follow(T)={+,),#}
Follow(B)={+,),#}
Follow(F)={*,+,),#}
构造Select集合
通过已有的first和follow我们可以比较简单地构造出select集合
定义与作用:Select集是针对产生式而言,对于一个产生式,它所产生的句子的句首符号所构成的集合称为Select集。其作用就是用于构建预测分析表,以便之后分析时选择正确的产生式。
有了前面First集和Follow集的构造,Select集合的构造就相对比较简单了,它有两种情况:
- 第一种是产生式能产生一个句子,但是不能推导出ε,则Select(E->α)=First(α)
- 第二种是产生式能推导出ε,则Select(E->α)={First(α)-ε} + Follow(E)
继续以那个为例子
line1:只有一个候选产生式,且E无法推导出ε,所以Select(E->TA) = First(T)
line2:第二行有两个候选式,针对第一个候选式A->+TA,因为以+开头,那么肯定就推不出ε,故Select(A->+TA)=+,而第二个产生式能推出ε,故Select(A->ε) = Follow(A)
line3:与第一行类似,略
line4:与第二行类似,略
line5:针对第一个产生式F->i,满足第一条规则,所以Select(F->i)=i;针对第二个产生式也是如此
Select(E->TA)= ['i', '(']
Select(A->+TA)= ['+']
Select(A->ε)= ['#', ')']
Select(T->FB)= ['i', '(']
Select(B->*FB)= ['*']
Select(B->ε)= ['+', '#', ')']
Select(F->i)= ['i']
Select(F->(E))= ['(']构建预测分析表
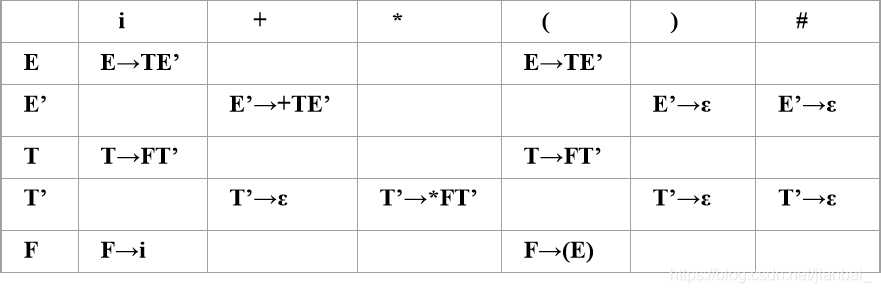
行(非终结符号):E,E’,T,T’,F
列(终结符号):i,+,*,(,),#
填写:非终结符号U+输入符号a->下一条执行的产生式
LR语法分析
概述
- 上下文无关文法的LR分析法
- LR:自左至右扫描,最右推导的逆过程(也就是最左归约)
在归约的过程中,一方面记住移入和归约的整个符号串,另一方面通过产生式推测未来可能碰到的输入符号
优缺点:
优点:文法范围广,识别能力强,可以识别出错位置
缺点:工作量大,需要构造这种分析程序的产生器
产生器作用:
应用产生器产生一大类上下文无关文法的LR分析程序
对二义性文法或难分析的特殊方法,施加一些限制使之能用LR分析法
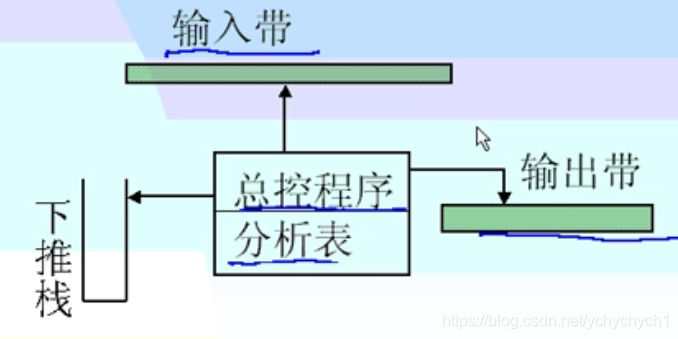
包括两部分:总控程序,分析表
总控程序:控制程序的运行,查分析表的内存做简单动作
产生器的任务就是产生分析表
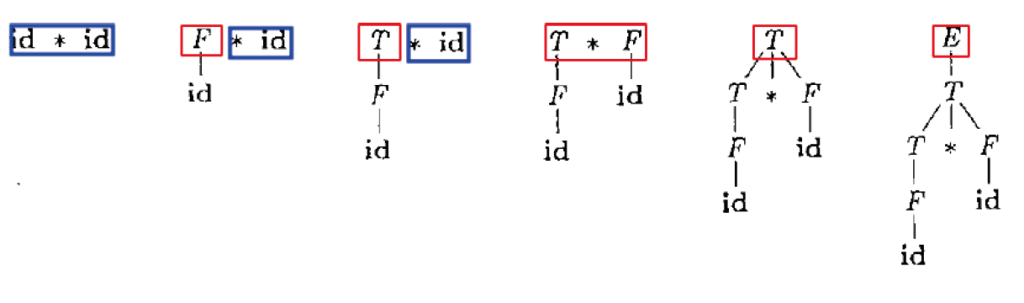
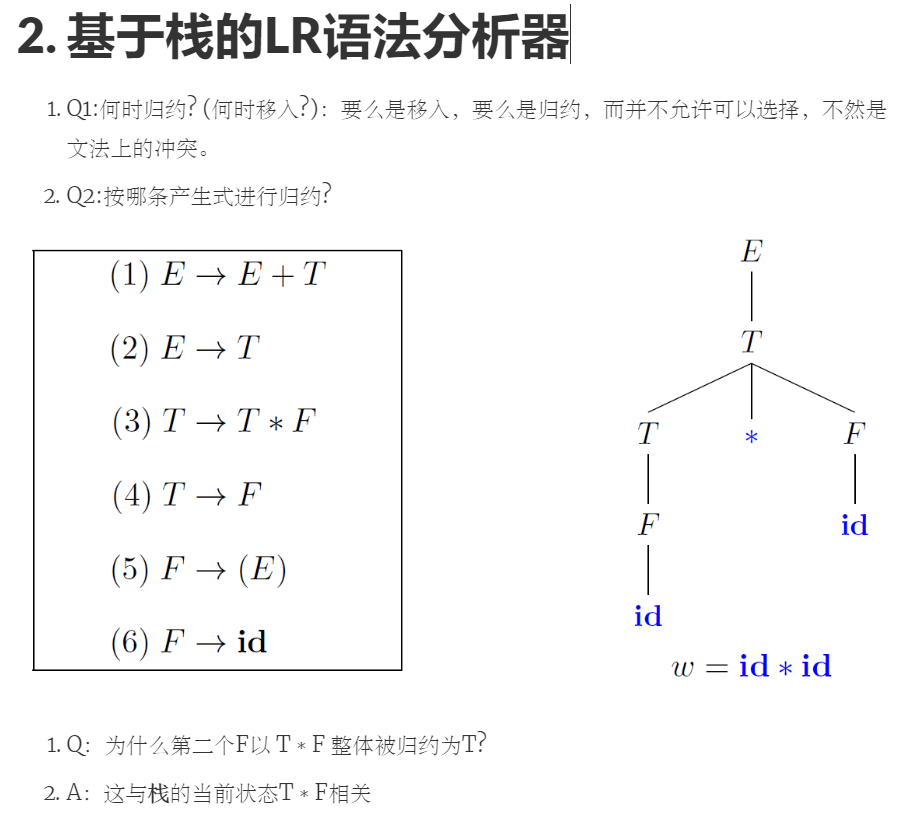
栈操作如下图所示:标号不是状态,仅表示顺序
| 时间序号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 栈顶 | id | F | ||||||||||||
| * | * | * | * | |||||||||||
| 栈底 | id | F | T | T | T | T | T | T | E |
- 两大操作: 移入输入符号与按产生式归约
- 直到栈中仅剩开始符号S, 且输入已结束, 则成功停止
- LR分析法的基本思想
- 规范归约时,当一串貌似句柄的符号串呈现于栈顶,LR分析法根据三方面来寻找句柄:历史,展望,现实

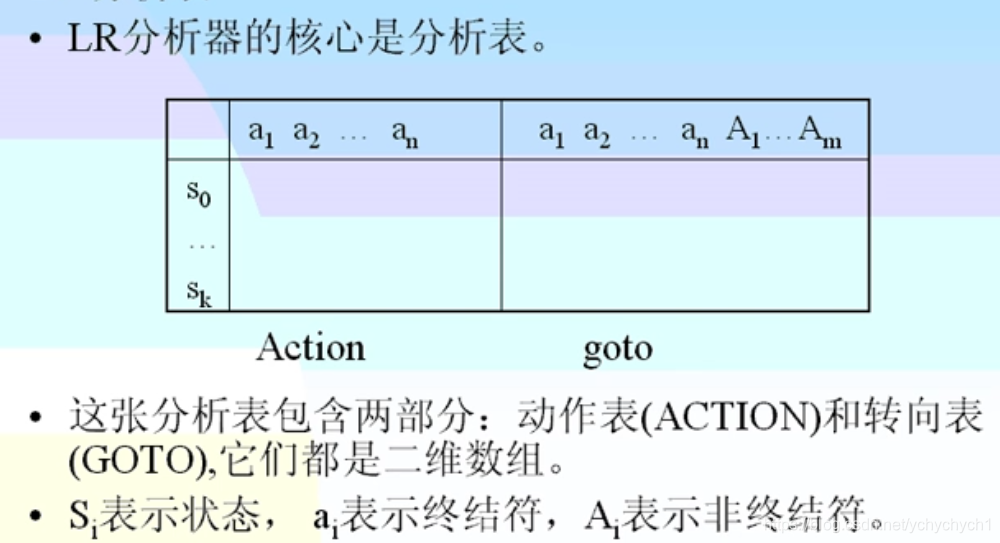
LR分析表指导LR语法分析器

- 在当前状态(编号)下, 面对当前文法符号时, 该采取什么动作
- ACTION表指明动作, GOTO表仅用于归约时的状态转换
- LR(0)、SLR(1)、LR(1)、LALR(1)的分析表会略有差异,加强规则会使其可以处理更多的文法。



LR(0)文法
项目的构造
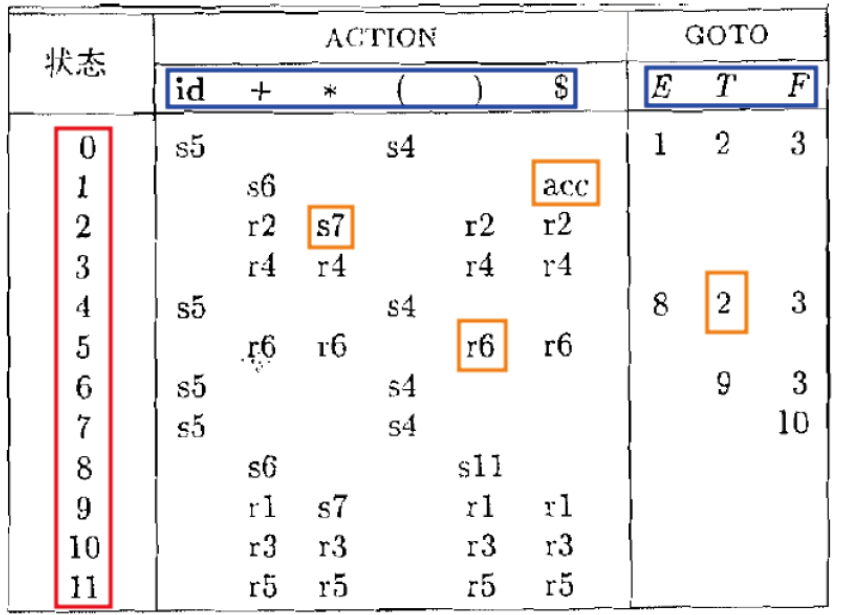
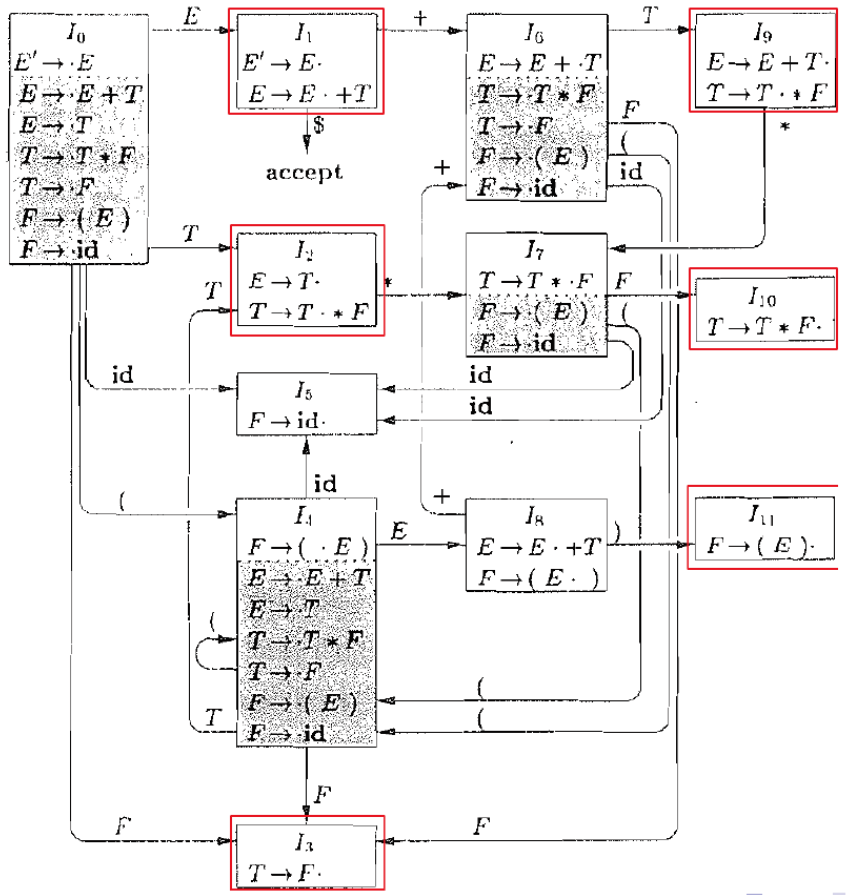
状态的序号在LR语法分析表中是通过构造规范LR(0)项目集族(canonical collection of LR(0) items)时顺序赋予的,每个状态对应一个项目集。这些序号是从0开始的递增整数,表示项目集族中的不同项目集。序号本身并没有固定的含义,只是表示项目集的顺序号。因此,状态5之所以是5,是因为在构造项目集规范族时,它被分配了这个数字。在另一个构造过程中,同样的项目集可能会被赋予不同的序号,只要在整个分析过程中保持一致即可。
具体步骤如下:
- 构造初始项目集:通常从包含开始符号的项目集开始,称为I0,分配状态号0。
- 递归构造其他项目集:
- 从I0出发,应用所有可能的文法符号(终结符和非终结符)构造新的项目集。
- 每次构造新的项目集时,检查它是否已经存在于当前的项目集族中。如果存在,则使用已存在的项目集的状态号;如果不存在,则分配一个新的状态号(下一个未使用的整数)。
- 确定状态序号:
- 序号是构造项目集时按顺序分配的。例如,初始项目集为0,下一个构造的项目集为1,再下一个为2,以此类推。
- 在构造的过程中,可能需要对同一个项目集多次应用goto操作,构造多个新的项目集,这些项目集分别分配不同的状态号。


由项目构造NFA的方法:

文法拓展的必要性:通过对文法的扩展,不会出现单单只识别了一个开始符号就确定是这个句子的情况。例如S->bS’A | asd,这时候,当我们,读入了b,进入bS‘A状态,然后需要读入S’,这时我们返回去,通过读入asd进入了终态,这时候,我们结束,但是也可以继续,这时候机器就不知道怎么选择了


例题:

句柄
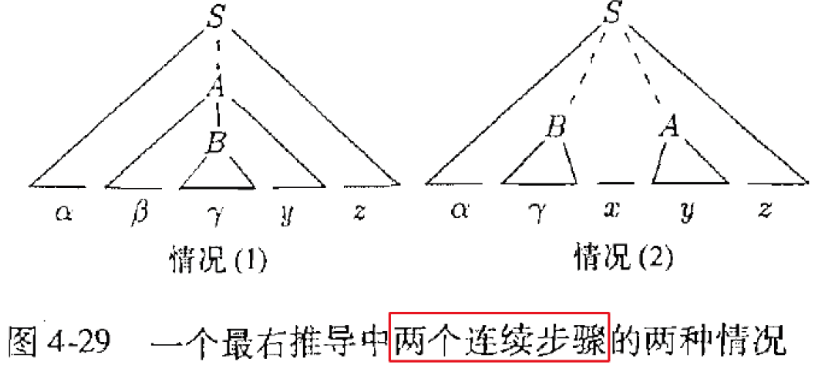
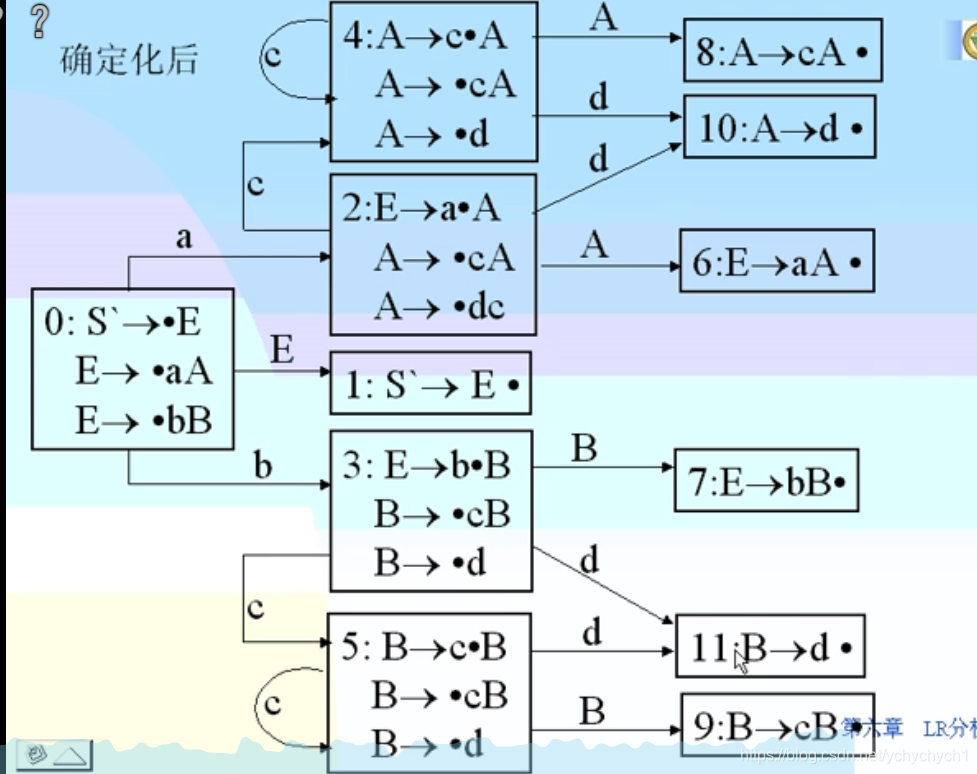
在输入串的(唯一)反向最右推导中, 如果下一步是逆用产生式将规约为, 则称是当前句型的句柄。
句柄可能在哪里?
Theorem:存在一种LR语法分析方法,保证句柄总是出现在栈顶
句柄出现在栈顶极大程度上方便了我们进行分析。
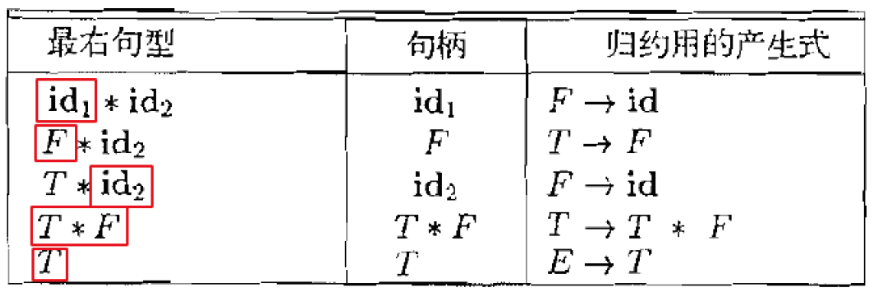
- 对于最右推导,任何推导都只有如上两种情况(注意是两次连续推导)
- A是B的父亲(等价于B是A的父亲)
- 或者A和B平级
- 情况2中的x必然为终结符(最右推导),每次规约后我们都可以在栈顶找到终结符。
- 可以用自动机跟踪状态变化(自动机中的路径 栈中符号/状态编号)
- 在自动机的当前状态识别可能的句柄(观察到的完整右部)(自动机的当前状态 栈顶)
- LR(0) 句柄识别有穷状态自动机(Handle-Finding Automaton)
语义分析
在G P L中,大部分的代码都具有多层的作用域,意味着每个变量都有自己的生效的范围
所以关于作用域一共有三类:全局,本地(local),函数作用域
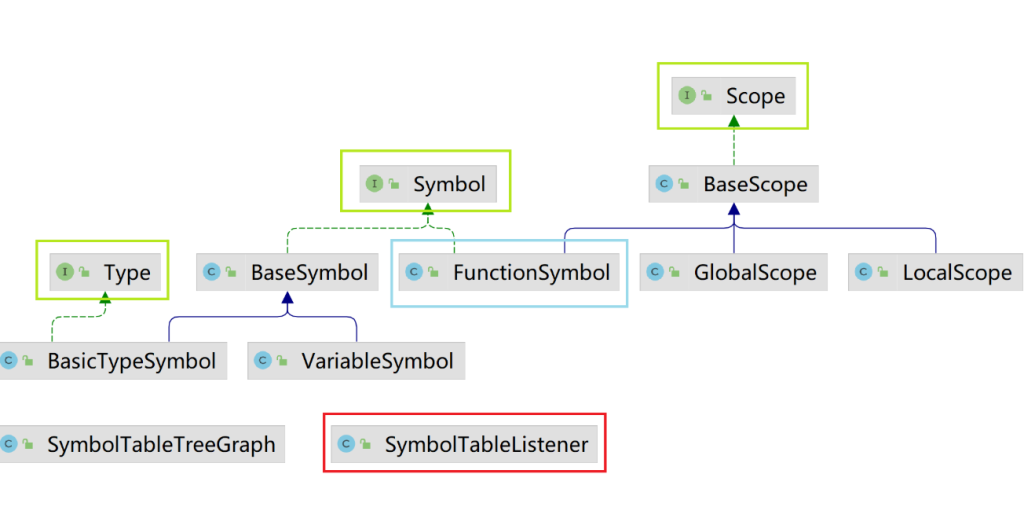
使用resolve寻找定义(依次遍历向上)
使用listener重写一些enter规则,比如在重写函数方法时,由于函数会开辟新的作用域,本身又是个符号,所以需要两种操作一起,先获取函数名之后开新的scope,并且在符号表之中加边。
语法制导翻译方案(SDT)
语义动作可以嵌入在产生式体中的任何地方
语法制导定义
语法制导定义是一个上下文无关文法和属性及规则的结合

属性文法简单来讲就是:
为每个文法符号(终结符或非终结符)配备若干相关的“值”(称为属性)。 对每个文法的每个产生式配备了一组属性的语义规则,对属性进行计算和传递。
.val属性用来存放这些非终结所对应的那部分表达式,如子表达式,项,因子等。
lexval表示,词法分析返回的单词的值。
在语法分析过程中实现属性文法
B →X{a}Y
语义动作嵌入的位置决定了何时执行该动作
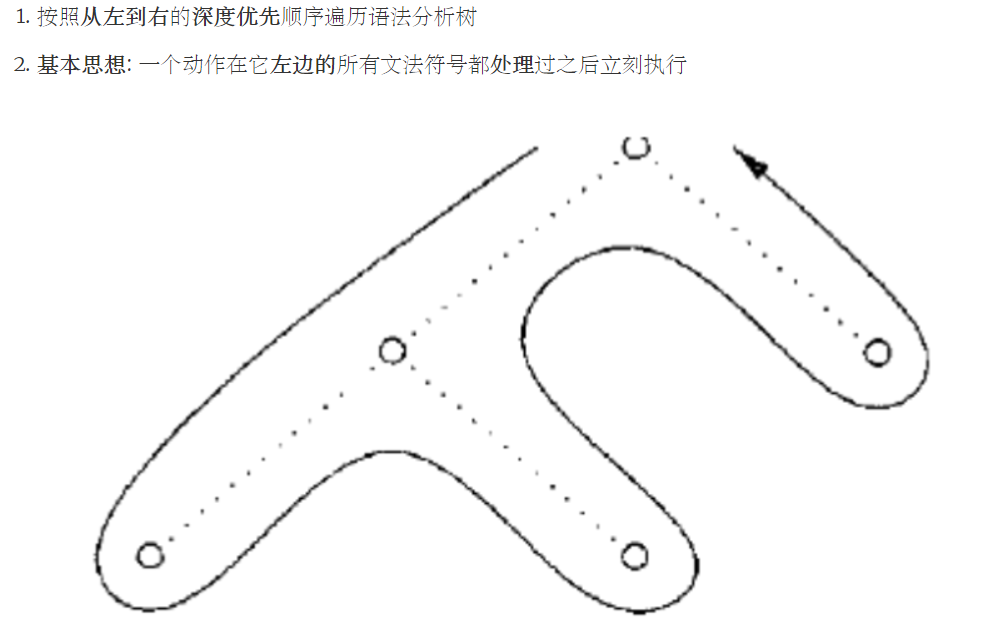
基本思想: 一个动作在它左边的所有文法符号都处理过之后立刻执行

嵌入语义动作虚拟节点的语法分析树
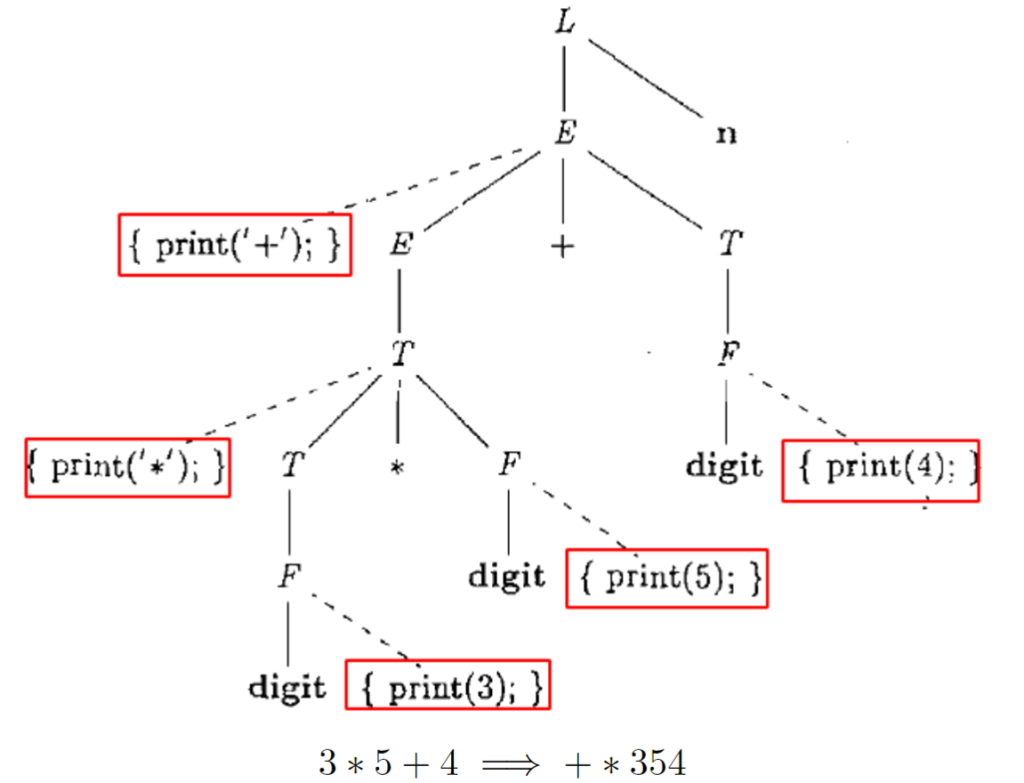
举个例子:

(a) 写一个翻译方案,它输出每个 a 的嵌套深度。例如,对于句子 (a, (a, a)),输出的结果是 1 2 2。
文法符号S,L继承属性depth表示嵌套深度,则翻译方案如下:

语义动作可以嵌入在产生体的任何位置,比如说把一些print操作放在产生式中间或者前面
前缀表达式SDT
- 语义动作嵌入的位置决定了何时执行该动作
- 基本思想: 一个动作在它左边的所有文法符号都处理过之后立刻执行
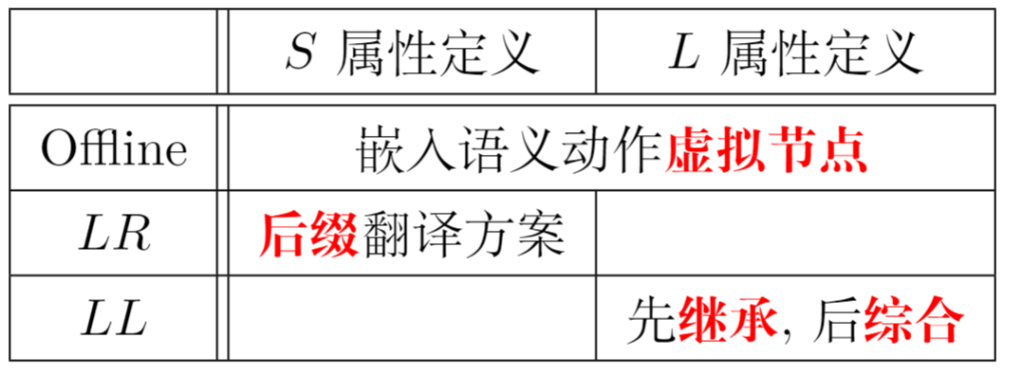
如何将SDD中的语义规则转换为带有语义动作的SDT?
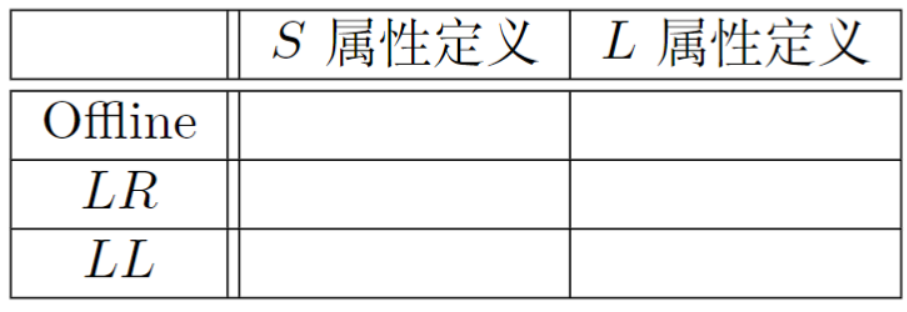
Offline 方式: 已有语法分析树
嵌入语义动作虚拟节点的语法分析树
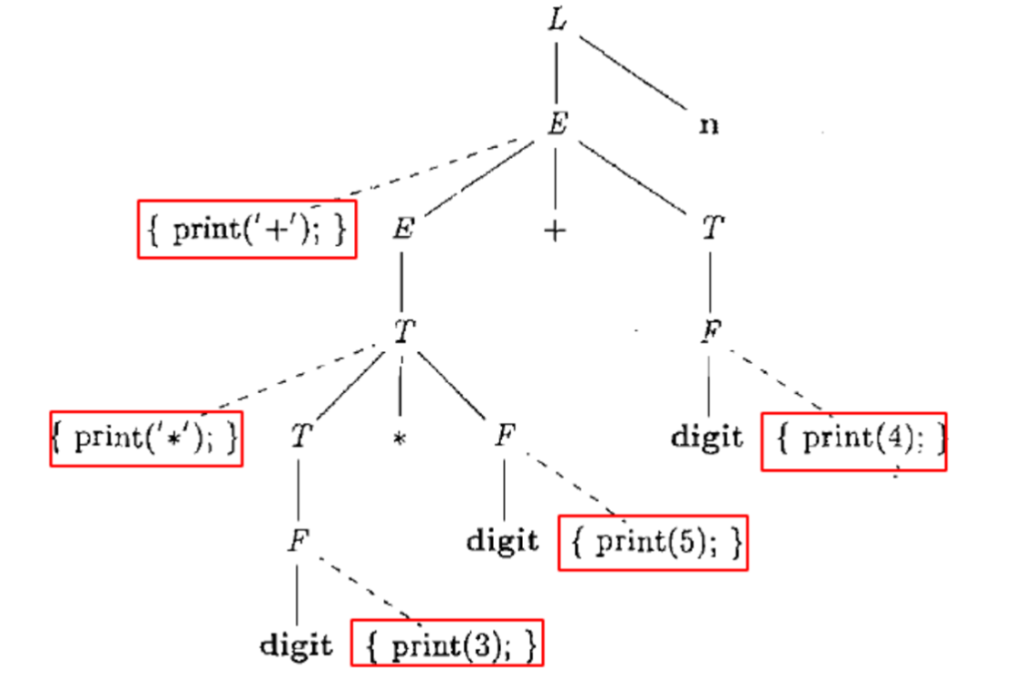
这个其实就是offline的一个做法,即在语法树中嵌入语义动作虚拟节点并且按上述顺序进行遍历然后执行这些虚拟节点

- 如何判断某SDT是否可以在LL/LR语法分析过程中实现?
- 将每个内嵌的语义动作A替换为一个独有的非终结符M,添加新产生式M→ε,判断新产生的文法是否可用LL/LR进行分析
后缀翻译方案:所有动作都在产生式的最后在LR中,按某个产生式归约时,执行相应动作
总结下来就是
中间代码生成
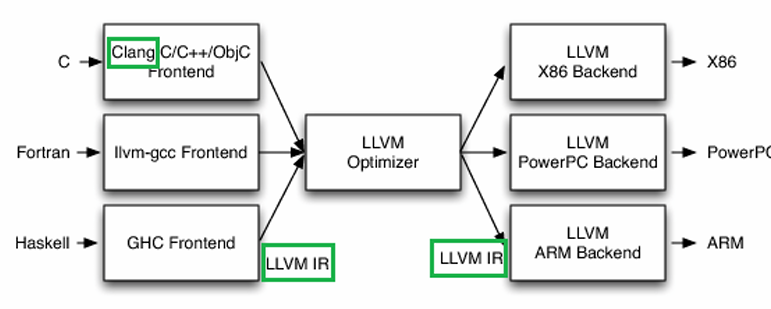
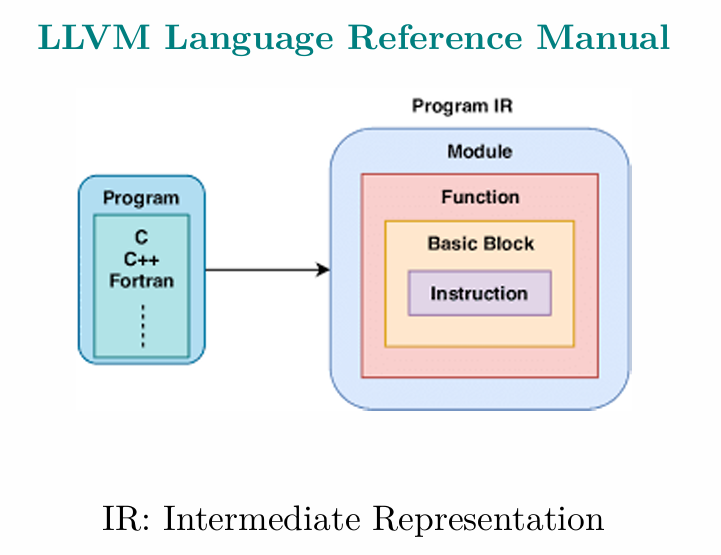
LLVM IR(Intermediate Representation)是一种中间语言表示,作为编译器前端和后端的分水岭。LLVM 编译器的前端——Clang 负责产生 IR,而其后端负责消费 IR。
编译器 IR 的设计体现了权衡的计算思维。低级的 IR(即更接近目标代码的 IR)允许编译器更容易地生成针对特定硬件的优化代码,但不利于支持多目标代码的生成。高级的 IR 允许优化器更容易地提取源代码的意图,但不利于编译器根据不同的硬件特性进行代码优化。
LLVM IR 的设计采用common IR和specific IR相结合的方式。common IR旨在不同的后端共享对源程序的相同理解,以将其转换为不同的目标代码。除此之外,也为多个后端之间共享一组与目标无关的优化提供了可能性。specific IR允许不同的后端在不同的较低级别优化目标代码。这样做,既可以支持多目标代码的生成,也兼顾了目标代码的执行效率。

当谈到编译器设计中的中间表示(IR)时,三地址码(TAC)和静态单一赋值形式(SSA)是两种常见的形式。详细介绍一下它们的区别:
- 三地址码(TAC):
- TAC是一种通用的中间表示形式,用于将高级语言代码转换为更低级的表示形式。
- 每条TAC代码最多有三个地址,其中两个是源地址,一个是目的地址。每条代码最多包含一个操作符。
- TAC主要用于生成代码,将高级语言翻译成汇编或机器代码。
- 静态单一赋值形式(SSA):
- SSA是一种特定的中间表示形式,具有一些特定的属性。
- 在SSA中,每个变量只能在一个地方被定义,且每个变量只能被赋值一次。
- SSA主要用于优化编译器的分析和转换,例如数据流分析、循环优化等
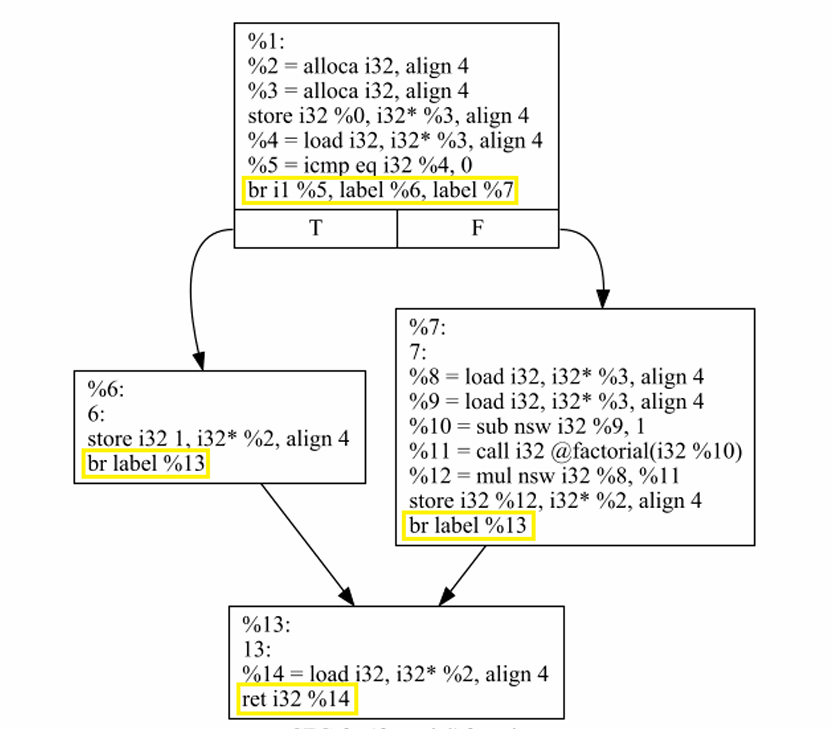
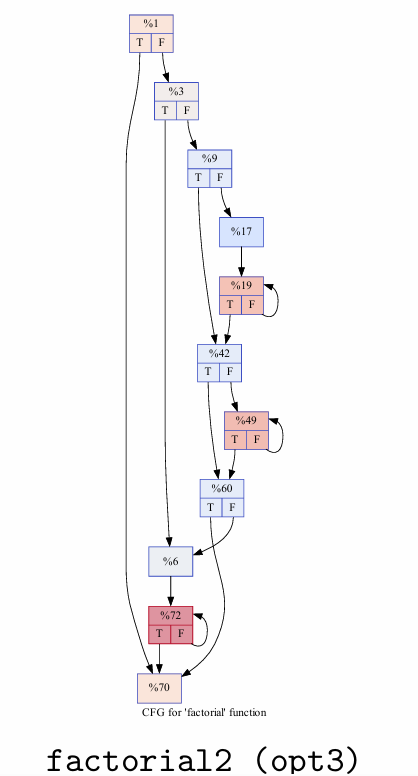
CFG的定义
Each node represents a basic block, i.e. a straight-line code sequence with no branches/jumps in except to the entry point and no branches/jumps out except at the exit point.
Jump targets start a block, and jumps end a block.
Directed edges are used to represent jumps in the control flow.


LLVM IR 有如下 3 种等价形式:
- 内存表示
- 类
llvm::Function、llvm::Instruction等用于表示common IR。 - 类
llvm::MachineFunction、llvm::MachineInstr等用于表示specific IR。
- 类
- 位码文件(Bitcode Files,存储在磁盘中)
- 汇编文件(Assembly Files,存储在磁盘中,便于人类可读)
call指令可以存在于一个基本块的中间,每个基本块都以一个终结符为结尾,代表这一个block必须在上一个block完全执行完之后才能执行,call这一点与要求不符合,所以并不需要另起block
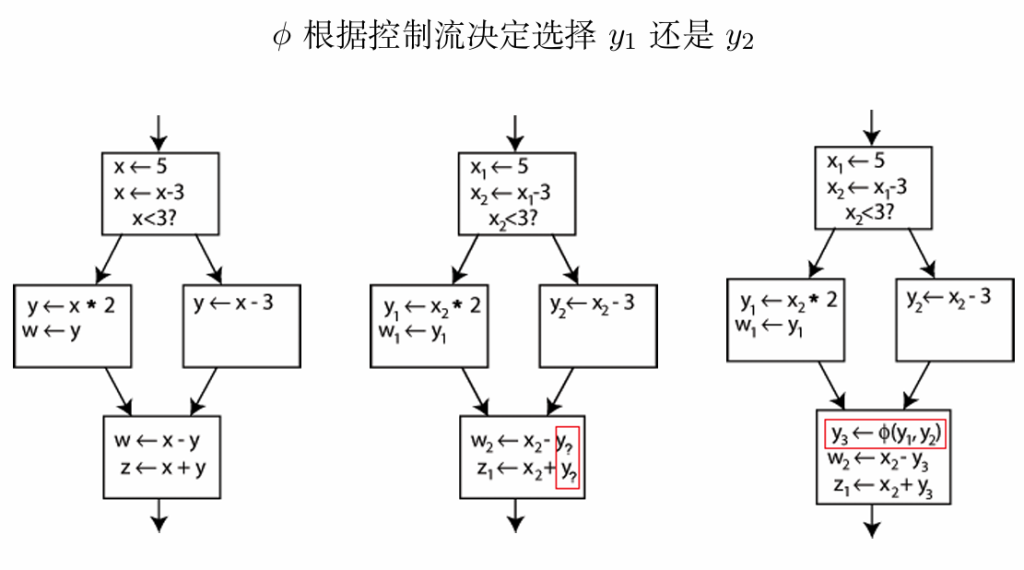
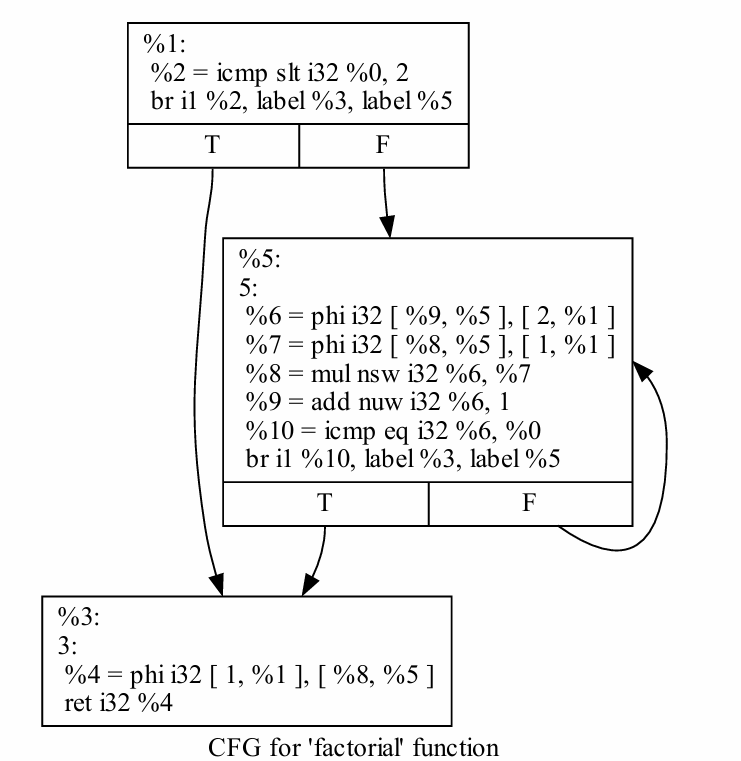
如何实现phi指令?
基本思想: 将ϕ指令转换成若干赋值指令,上推至前驱基本块中
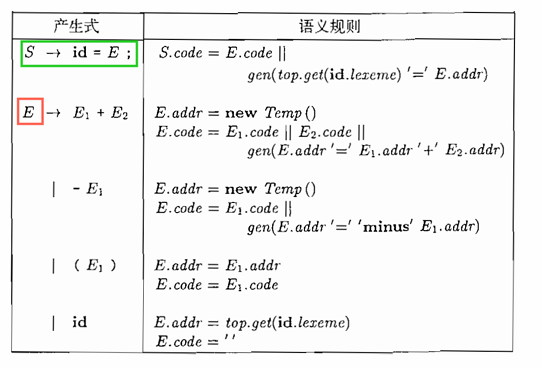
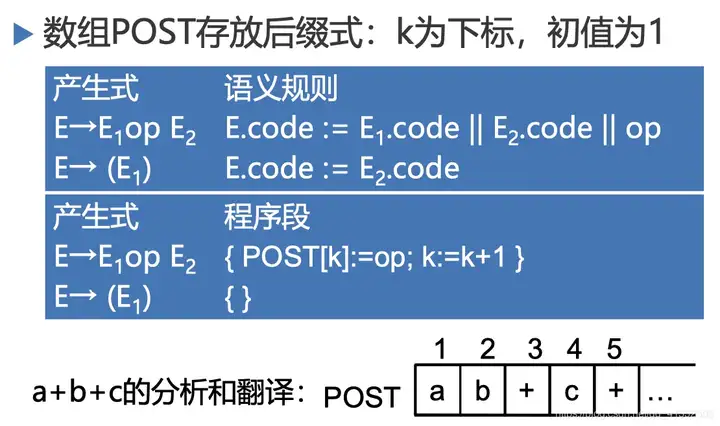
综合属性E.addr:变量名(包括临时变量)、常量
表达式 => 后缀式的属性文法



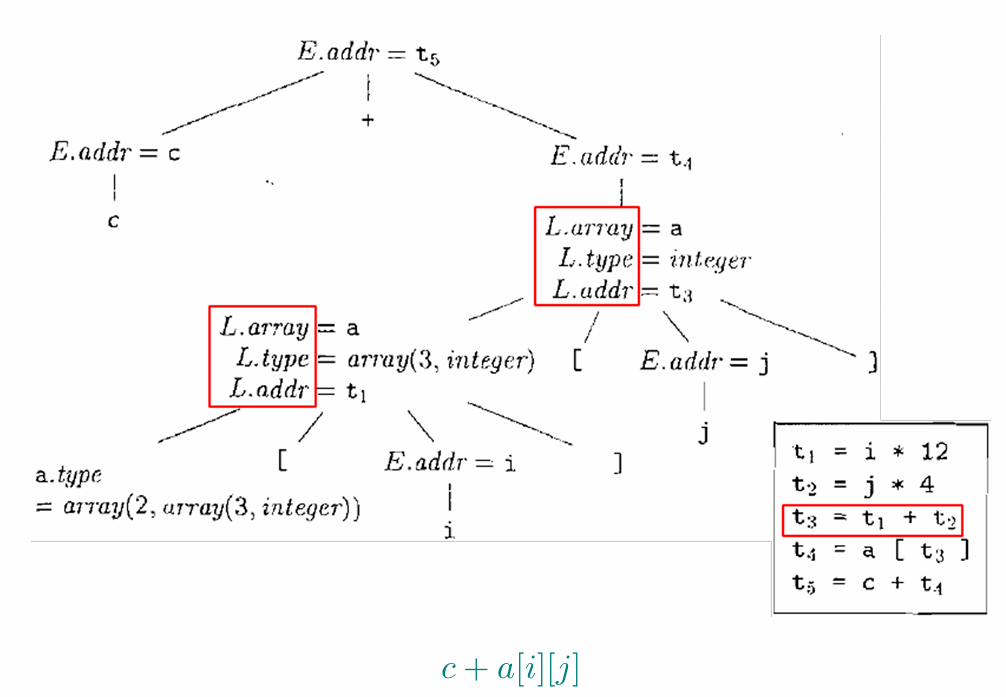
GEP provides a way to access arrays and manipulate pointers.
getelementptr的语法如下:<result> = getelementptr <ty>, <ty>* <ptrval> {, [inrange] <ty> <idx>}*<result>是计算结果的变量。<ty>是类型。<ptrval>是指针操作数。<idx>是索引,用于“遍历”指针操作数。
getelementptr主要用于数组和结构体的元素访问。它可以根据索引计算出元素的地址。例如,如果有一个整型数组arr,我们可以使用以下代码获取第三个元素的地址:%ptr = getelementptr i32, i32* %arr, i64 2